Flat-Earthers like to use the erroneous “8 inches per mile squared” to calculate the height hidden by Earth’s curvature. The following is the correct equation for the purpose, accounting for the observer’s height & atmospheric refraction
Refraction Effect on the Lake Pontchartrain Power Transmission Line
The strength of atmospheric refraction is not constant but varies depending on the weather condition. As a result, a distant object usually obscured by Earth’s curvature can sometimes be visible if the refraction is strong enough.
Lake Pontchartrain transmission towers demonstrate Earth’s curvature. Flat-Earthers like to cherry-pick moments where the towers appear straight, ignoring other cases. In reality, they look straight only because the refraction was strong enough.
Continue reading “Refraction Effect on the Lake Pontchartrain Power Transmission Line”
Pic Gaspard
The photo of Pic Gaspard taken from Pic de Finestrelles is one of the farthest line-of-sight photos of an object on Earth’s surface, taken from another location on Earth’s surface. It is possible to take the photo due to the height of the peaks & atmospheric refraction.
The apparent height of Pic Gaspard relative to the other peaks proves Earth is a sphere. If Earth were flat, Pic Gaspard should appear higher than Grand Ferrand from the observer’s location. Simulations also give us the same results as observation, confirming that it is really what would look like on a spherical Earth.
Perspective and the Lake Pontchartrain Transmission Line
The Lake Pontchartrain power transmission pylons demonstrate Earth’s curvature. Flat-Earthers invented various excuses to dismiss the observation, including the excuse that it was just a perspective effect.
If it were just a perspective effect, the same parts of the pylons would line up in a straight line, converging into a distant point. In reality, they do not line up in a straight line but are visibly curving downward due to the curvature of the Earth.
Continue reading “Perspective and the Lake Pontchartrain Transmission Line”
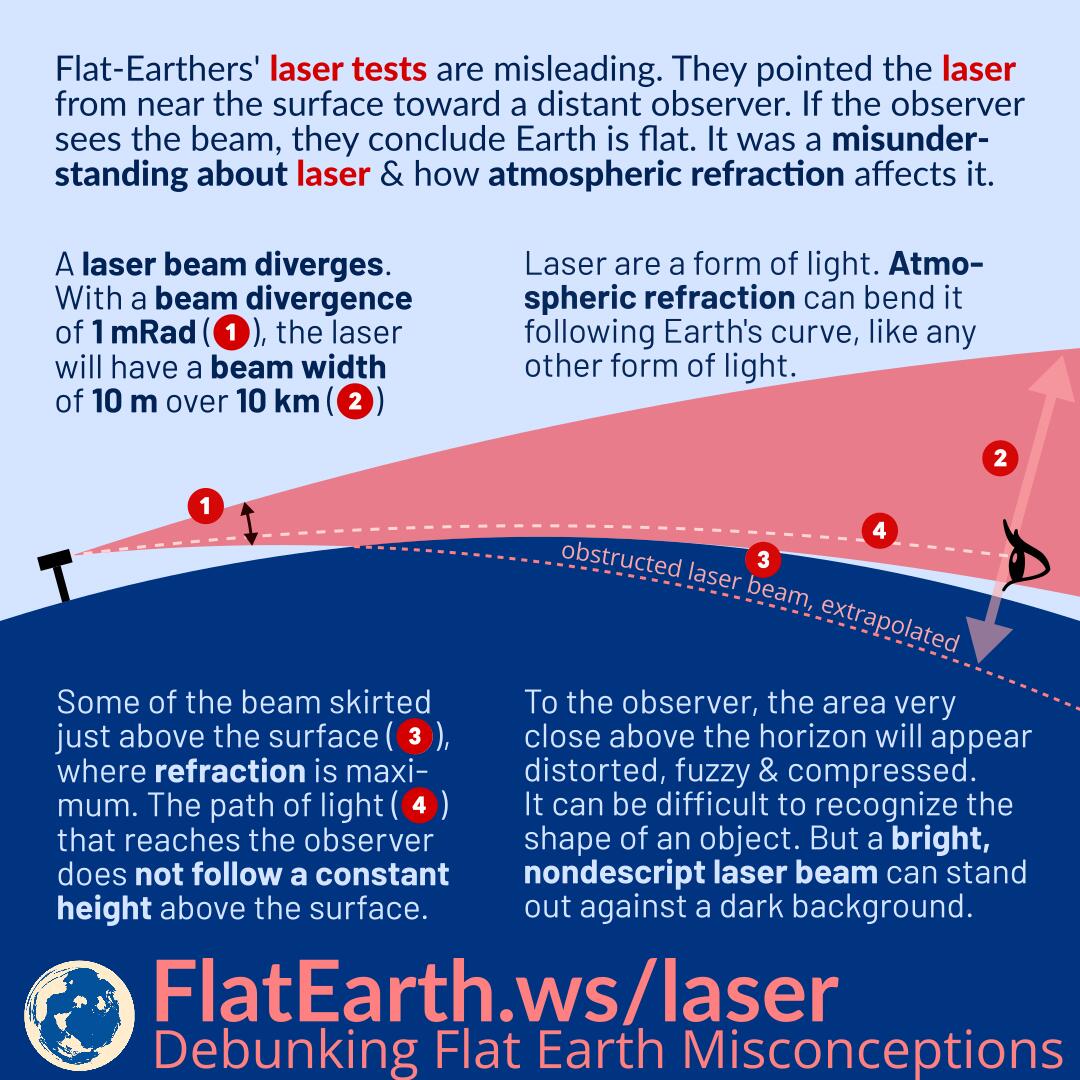
Flat-Earth Laser Tests are Misleading
Flat-Earthers’ laser tests are misleading. They pointed the laser from near the surface toward a distant observer. If the observer sees the beam, they conclude Earth is flat. It was a misunderstanding about laser & how atmospheric refraction affects it.
Different Reasons Why a Distant Object is Not Visible
Different reasons can cause a distant object to be not visible:
- The angular resolution limit of the observer.
- The visibility limit imposed by the atmosphere.
- Obstruction by another object, including by Earth’s curvature.
Flat-Earthers incorrectly presumed “a distant ship is not visible only because of Earth’s curvature.” Incorrectly concluded if we can bring the ship back into view, the curve must not exist. In reality, Earth’s curvature is not the only thing that can cause a distant ship to be not visible; other reasons can also cause it.
Continue reading “Different Reasons Why a Distant Object is Not Visible”
Flight Instruments
Pilots can easily observe that Earth is a sphere, either by visual observation or from the aircraft’s flight instrument.
The level indicator is above the visible horizon. It is the dip of the horizon caused by the fact that Earth is a sphere. Earth’s horizon itself is visibly curving. The horizontal component of the velocity vector is often not the same as the plane’s direction due to the wind & the Coriolis effect from Earth’s rotation.
Lake Pontchartrain’s Horizon Curvature
The Lake Pontchartrain causeway and transmission lines demonstrate Earth’s curvature. Flat-Earthers attempt to dismiss it using aerial photos where it is more difficult to see the curved landmarks over water.
On the other hand, from these alternative vantage points, it becomes easier to reveal the horizontal curvature by magnifying vertically. Because of the possibility of lens distortions, some of the images are inadequate evidence of the curve. However, all of them are insufficient evidence of a flat Earth.
Difference in Hidden Height Calculation Results
Flat-Earthers use “8 inches per mile squared” to calculate the hidden height of a distant object. It is not the proper formula as it ignores the observer’s height & refraction. It will result in an erroneously larger hidden height than the correct amount.
A 2-m-tall observer will be able to see a 5-m-high object at 10 km. However, the 8-inches rule erroneously tells it should be entirely hidden. It is the source of a lot of flat Earth misinformation.
Continue reading “Difference in Hidden Height Calculation Results”
Fisheye Lenses and Lens Distortions
A photographic lens may have a specific distortion characteristic and strength that may differ from another lens. However, despite the differences, a straight line will always appear straight if it crosses the center of the frame.
Flat-Earthers like to dismiss images taken by a fisheye lens. In reality, the attributes of such a lens are well known. We can use the knowledge to determine if a line in the image is straight, even if it was taken using a fisheye lens.
Thompson vs. Garcia, 2019
Thompson vs. Garcia was a lawsuit about a “contest to prove Earth’s curve” set up by the defendant, a flat-Earther. The plaintiff felt he had won the contest & the defendant failed to pay. The plaintiff did provide evidence of Earth’s curvature, but not in the way required by the contest. Thus, the court ruled in favor of the defendant.
Glass of Water
Earth’s gravity causes water’s surface to curve with the same radius as Earth’s. On glass with a diameter of 10 cm, Earth’s gravity causes the water to form a curvature of 0.00000002 cm, outside other factors like surface tension.
Flat-Earthers like to demand that we prove water curvature in a glass of water. In reality, whatever the container, the curvature of the water surface remains the same as Earth’s radius. On a glass of water, it will be too small to observe.
Turning Torso Building, Malmö, Sweden
Turning Torso is a skyscraper in Malmö, Sweden, having a distinctive segmented shape & easy to recognize from far. From Copenhagen, Denmark, we can see its lower part is obscured more if we are farther because Earth is a sphere.
The building is close to the strait of Øresund. Copenhagen, Denmark, lies at the other side of the channel, only 15 km (9 miles) away from Malmö. Turning Torso has a distinctive segmented shape that is easy to recognize from far. And more importantly, for our purposes, its segmented form makes it easy to judge its height from far.
First Image of Earth From Space Taken By a V-2 Rocket
The first image of Earth from space was taken by the V-2 No. 13 rocket in 1946 using the DeFry 35mm movie film camera and a 50mm lens attached to the rocket. The camera had a relatively narrow field of view. As a result, Earth’s curvature is only very slightly visible.
Flat-Earthers claim the flat appearance in the photo “proves” a flat Earth. In reality, 1. by careful examination, we can see the curve, 2. the camera has a narrow field of view, reducing the visible curvature, 3. the photo shown by flat-Earthers is usually a cropped version, further reducing the visible curve, and 4. the photo matches the expected curvature according to simulation.
Continue reading “First Image of Earth From Space Taken By a V-2 Rocket”
The Wallace Method
In 1870, Alfred Russel Wallace proved Earth’s curvature in the Bedford level experiment. His method was straightforward & effective and can be easily used in a similar experiment.
Wallace’s method fixes the common issues with similar experiments done by flat-Earthers. They usually fail to control, and even disregard, the effect of atmospheric refraction. Using Wallace’s simple method, we can easily prove Earth is a sphere.
Magnitude of Visible Earth’s Curvature in a Photograph
The magnitude of the curvature that appears in a photograph of Earth’s curvature depends on several factors:
- The observer’s altitude.
- The camera’s field of view or focal length.
- The distortion characteristics of the camera lens.
Flat-Earthers like to dismiss a photo of Earth’s curvature by comparing it to another photo showing a different amount of curvature. In reality, to compare the visible curvature, we need to ensure all the images were taken from the same altitude, same field of view, and account for the lens’ distortion.
Continue reading “Magnitude of Visible Earth’s Curvature in a Photograph”
Danyang–Kunshan Grand Bridge
As of 2021, the Danyang–Kunshan Grand Bridge is considered the longest bridge in the world. It is a 164.8-km-long viaduct bridge in China, consisting of 2000 spans of ~80 m long each. Like every other bridge, it is constructed following Earth’s curvature.
A hoax in flat Earth communities claims the Danyang–Kunshan Grand Bridge somehow “proves” flat Earth. In reality, it is just a claim asserted without evidence and then spread as a hoax.
The bridge is a viaduct with many short spans, and therefore, accounting for Earth’s curve is less critical than in the case of longer-spanning bridges. Nevertheless, it is still built to follow Earth’s curvature.
Auguste Piccard, A Scientist Falsely Claimed by Flat-Earthers
In 1931, Auguste Piccard went up in a balloon to an altitude of 15781 m, not far above the cruising altitude of an airliner. At the altitude, Earth’s curvature is still very slight and difficult to see, especially through the small portholes in his chamber.
In a Popular Science interview, Piccard was reported to have said that Earth “seemed a flat disc with an upturned edge.” Flat-Earthers quickly interpreted his statement as if he was telling us Earth is flat. In reality, in another interview, it is clear that he is convinced that Earth is a sphere. In his writings about his expeditions, the word “globe” was also mentioned several times.
Continue reading “Auguste Piccard, A Scientist Falsely Claimed by Flat-Earthers”
Perspective Compression: Determining If a Curvature Exists
By utilizing perspective compression, it will be easier for us to observe the curvature of an object if the object is curved.
Flat-Earthers like to deliberately choose a vantage point where it is difficult to see Earth’s curvature, and they use it to “prove” the curvature does not exist. In reality, they only make it more difficult to see the curvature. It does not mean the curve is not there.
Continue reading “Perspective Compression: Determining If a Curvature Exists”
Bedford Level Experiment Confirmed the Curvature of the Earth
In 1870, Alfred Russell Wallace took a challenge from a flat-Earther and successfully confirmed the existence of Earth’s curvature in the Bedford level experiment.
Wallace did the experiment on the Bedford Canal. Wallace fixed a black band on the Old Bedford Bridge and observed it with a telescope from the Welney Bridge 6 miles away. Right in the middle, he placed a pole with two discs on it. The telescope, the top disc, and the black band are at the same height above the water.
From the telescope, both discs were seen above the black band, proving the existence of Earth’s curvature.
Continue reading “Bedford Level Experiment Confirmed the Curvature of the Earth”