Tag: archimedes

Archimedes’ Principle and Gravity

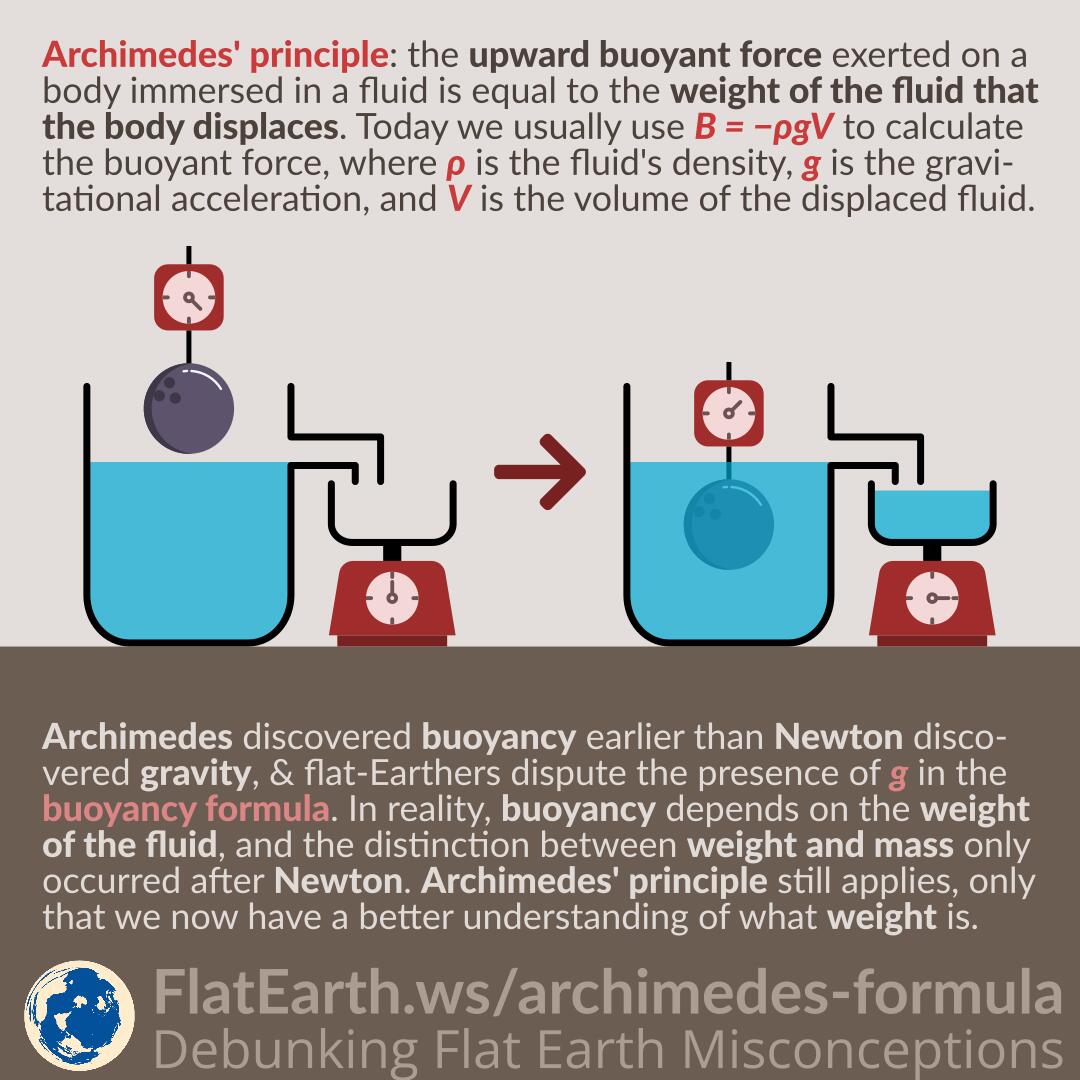
Archimedes’ principle states that any object, totally or partially immersed in a fluid, is buoyed up by force equal to the weight of the fluid displaced by the object. Meanwhile, Newton’s law of universal gravitation states that every particle attracts each other with force directly proportional to their masses & inversely proportional to the square of their distances.

Flat-Earthers like to characterize gravity as if it was “invented” to “replace” Archimedes’ principle & that the two are competing theories. In reality, these are two different theories that explain different phenomena. Gravity does not explain anything that Archimedes’ principle explains and vice versa. Gravity does not replace Archimedes’ principle; both are valid and in use today.

Continue reading “Archimedes’ Principle and Gravity”

Archimedes and the Surface of any Fluid

In the 3rd century BCE, Archimedes of Syracuse wrote what we now call the Archimedes’ principle in his book “On Floating Bodies” using the spherical Earth model.

Flat-Earthers like to misuse Archimedes’ principle as if it supports their claim that Earth is flat. In particular, they abuse Archimedes’ principle as if it is a competing explanation against gravity. In reality, Archimedes and other Greek scientists at the time already knew Earth is a sphere, and he explicitly mentioned it in his writings.

Continue reading “Archimedes and the Surface of any Fluid”

Gravitational Acceleration in Archimedes’ Formula

Archimedes’ principle states that the upward buoyant force exerted on a body immersed in a fluid is equal to the weight of the fluid that the body displaces. Today we usually use B =  -ρgV to calculate the buoyant force, where ρ is the fluid’s density, g is the gravitational acceleration, and V is the volume of the displaced fluid.

Archimedes discovered buoyancy earlier than Newton discovered gravity, and flat-Earthers dispute the presence of g in the buoyancy formula. In reality, buoyancy depends on the weight of the fluid, and the distinction between weight and mass only occurred after Newton. Archimedes’ principle still applies, only that we now have a better understanding of what weight is.

Continue reading “Gravitational Acceleration in Archimedes’ Formula”