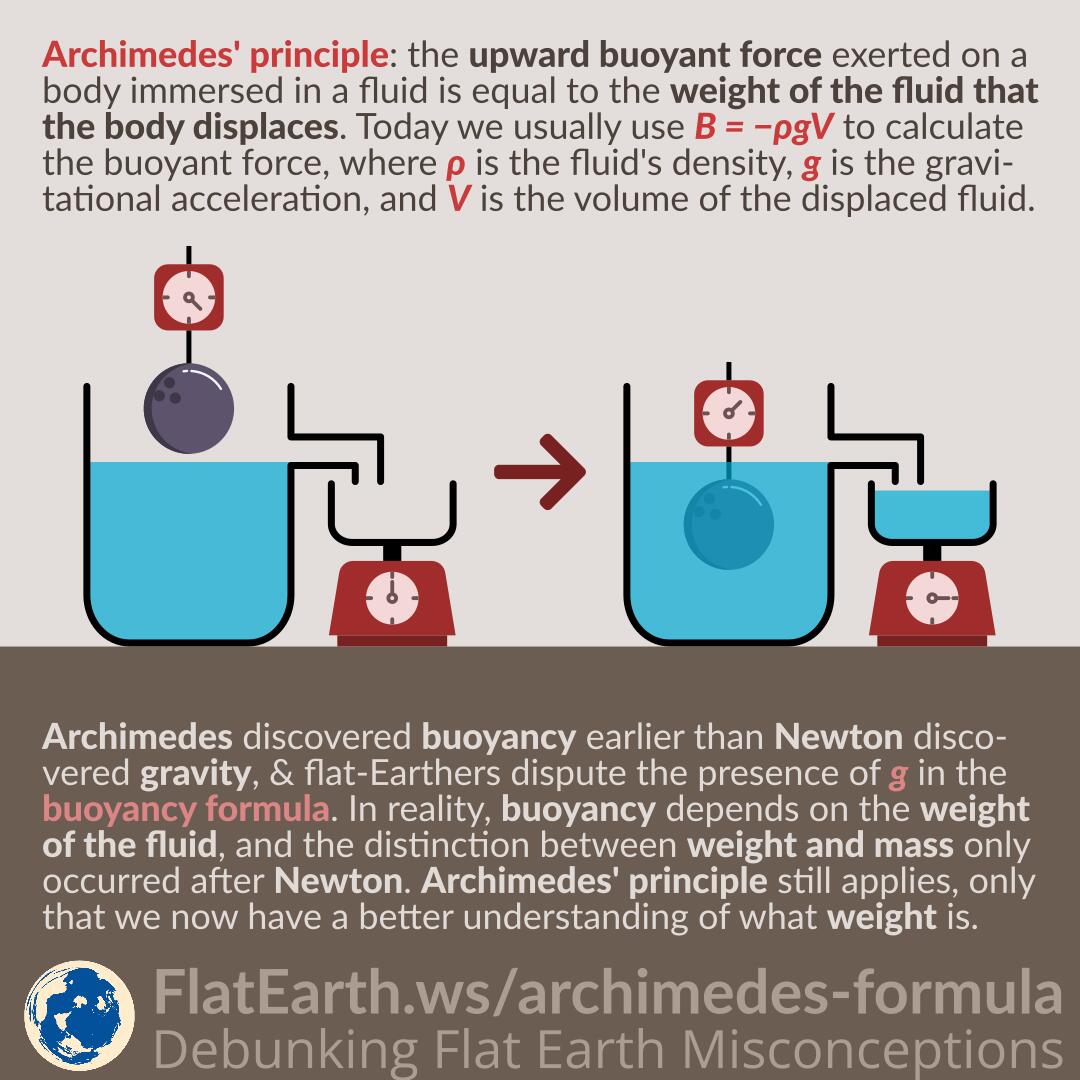
Archimedes’ principle states that the upward buoyant force exerted on a body immersed in a fluid is equal to the weight of the fluid that the body displaces. Today we usually use B = -ρgV to calculate the buoyant force, where ρ is the fluid’s density, g is the gravitational acceleration, and V is the volume of the displaced fluid.
Archimedes discovered buoyancy earlier than Newton discovered gravity, and flat-Earthers dispute the presence of g in the buoyancy formula. In reality, buoyancy depends on the weight of the fluid, and the distinction between weight and mass only occurred after Newton. Archimedes’ principle still applies, only that we now have a better understanding of what weight is.
Newton discovered that the weight of a body on Earth’s surface is caused by gravity exerted by Earth’s mass on the body. Because the strength of Earth’s gravity varies, the weight of an object also depends on its location on Earth. Due to this fact, Newton separated weight into mass and gravitational acceleration. Mass is an intrinsic property of a body whose magnitude is constant despite being affected by the varying strength of Earth’s gravity.
In Archimedes’ time, we only knew about weight, we have not yet discovered that weight is actually caused by gravity, and we did not know that weight varies depending on the location. Because the weight of an object can vary, then the magnitude of buoyancy also varies. The existence of g in the buoyancy formula is there to account for the difference.
References
- Archimedes’ principle – Wikipedia
- Mass versus weight – Wikipedia