In the 11th century, Al-Biruni successfully determined the radius of the Earth. He accomplished that by measuring the dip of the horizon from the top of a hill. From the measurements, he was able to calculate the radius of the Earth.
In the 21st century, we can easily repeat the same experiment with practically no effort. We just need a smartphone and an opportunity to observe the horizon from a high altitude, like during a flight.
Al-Biruni carried out his measurement in two steps.
First, he measured the height of a mountain. He took two measurements of the angle to the top of the mountain from two different locations. From the results, he was able to determine the height of the hill.
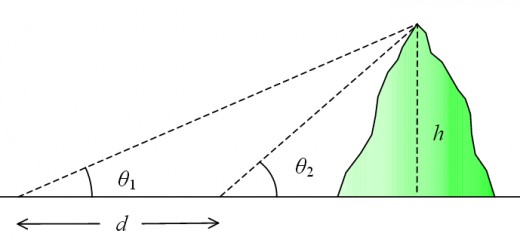
Second, he climbed to the top of the mountain and measured the dip of the horizon. From his measurements, he was able to calculate the radius of the Earth.

Using modern technology, we can carry out the same measurement and determine the radius of the Earth by ourselves. These days, practically all smartphones are equipped with GPS that can measure our altitude, and we can skip Al-Biruni’s first step. And with the accelerometer sensors inside our phones, we can measure the dip of the horizon. Using a smartphone that we already carry everywhere, we can carry out Al-Biruni’s measurement. We only need to be in a high enough location and a clear view of the horizon, like during a flight.
Make sure the app is already installed before boarding, and naturally, don’t forget to book a window seat! A measurement done over the ocean is more accurate. And if we don’t believe the altitude our smartphones are telling us, we can always ask a flight attendant or use the in-flight entertainment (IFE) system.
Table of Contents
Apps
These are some of the apps we can use to perform the measurement.
- Theodolite (iOS)
- Dioptra (Android)
- Geocam (Android)
- Surveyor Tools (Android)
Calculation
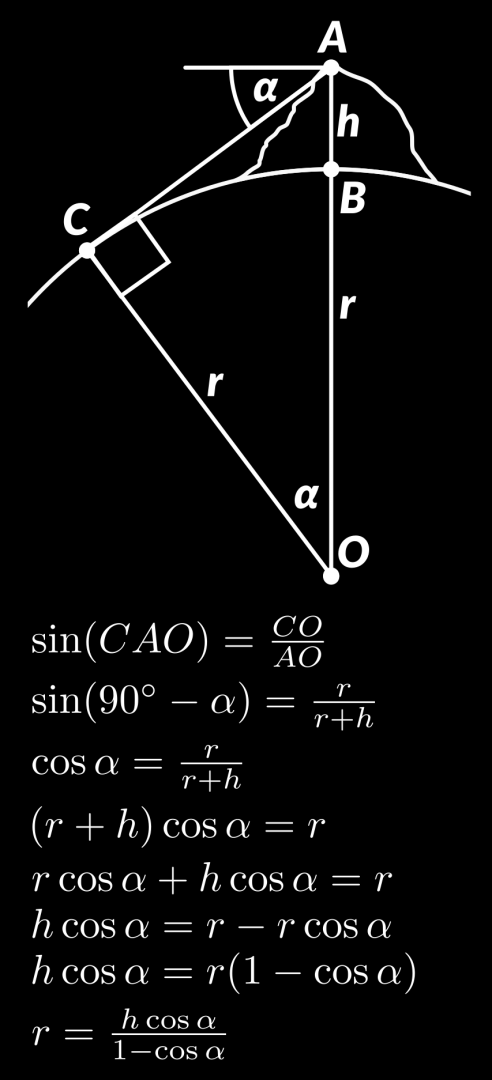
Calculation using the numbers in the illustration: 38805 ft * cos(3.4 degrees) / (1- cos(3.4 degrees)) in km = 6707.8 km
The result is different only about 5% from the actual value.
Derivation of the Equation
References
- Al-Biruni’s Classic Experiment: How to Calculate the Radius of the Earth – Owlcation
- The Empire of Reason 3/6 (Science and Islam – Episode 2 of 3) – Jim Al-Khalili – BBC
- How Al-Biruni Calculated the Circumference of the Earth Using a Mountain in the 11th Century – Flat Earth Busted


