The Reason We Cannot See Earth’s Curvature When Standing on a Beach

We can’t directly observe and subjectively perceive the curvature of the Earth from a position close to the surface. And this matches the expectations in the spherical Earth model.

Flat-Earthers often take the fact we can see the curvature by standing on a beach as ‘evidence’ the curve doesn’t exist. They are, once again, wrong.

Because the Earth is spherical, on a clear day, we can see the distinct horizon line. The distance from us to the horizon depends on our height from the surface. The higher we are from the surface, the farther is the distance to the horizon.

By standing on the shore, the height of our eyes from the surface is probably around 2 m (6.5 ft). As a result, the distance to the horizon is about 5 km (3.1 mi).

A human eye has the ‘cone of visual attention’ of about 55°. To account for variance (and to be generous too) we will make it 65°.  With a field of view of 65°, the length of the horizon from left to right is about 5.4 km (3.4 mi).

Because the Earth is spherical, the horizon line is curved. It does not appear curved to our eyes because with the length of5.4 km (3.4 mi), the bulge is only 58 cm (23 in), or only about 0.01 percent of the visible length of the horizon.

Flat-Earthers often confuse ‘practically flat’ with ‘perfectly flat’. We can’t see Earth’s curvature from the Earth surface itself, not because “there’s no curvature”, but because the curvature is too small for us to perceive.’

To directly observe the curvature, we need to go higher, much higher.

Distance to Horizon Calculation

(R+h)^2 = R^2 + d^2 \,\!\\ R^2 + 2Rh + h^2 = R^2 + d^2 \,\!\\ d = \sqrt{h(2R + h)} \,.

If the height of the observer from the surface of the water is 2 m, then we can determine the distance to the horizon:

d = \sqrt{2(2*6371000 + 2)} = 5048\,.

In Google Calculator: sqrt(2 * (2 * 6371000 + 2))

Apparent Horizon Length Calculation

Assuming a human eye’s field of view is 65°, then the length of the visible horizon = 2 * 5048 m * sin(65 degrees/ 2) = 5425 m

5048 m is the distance to the horizon as determined earlier.

Curvature Bulge Calculation

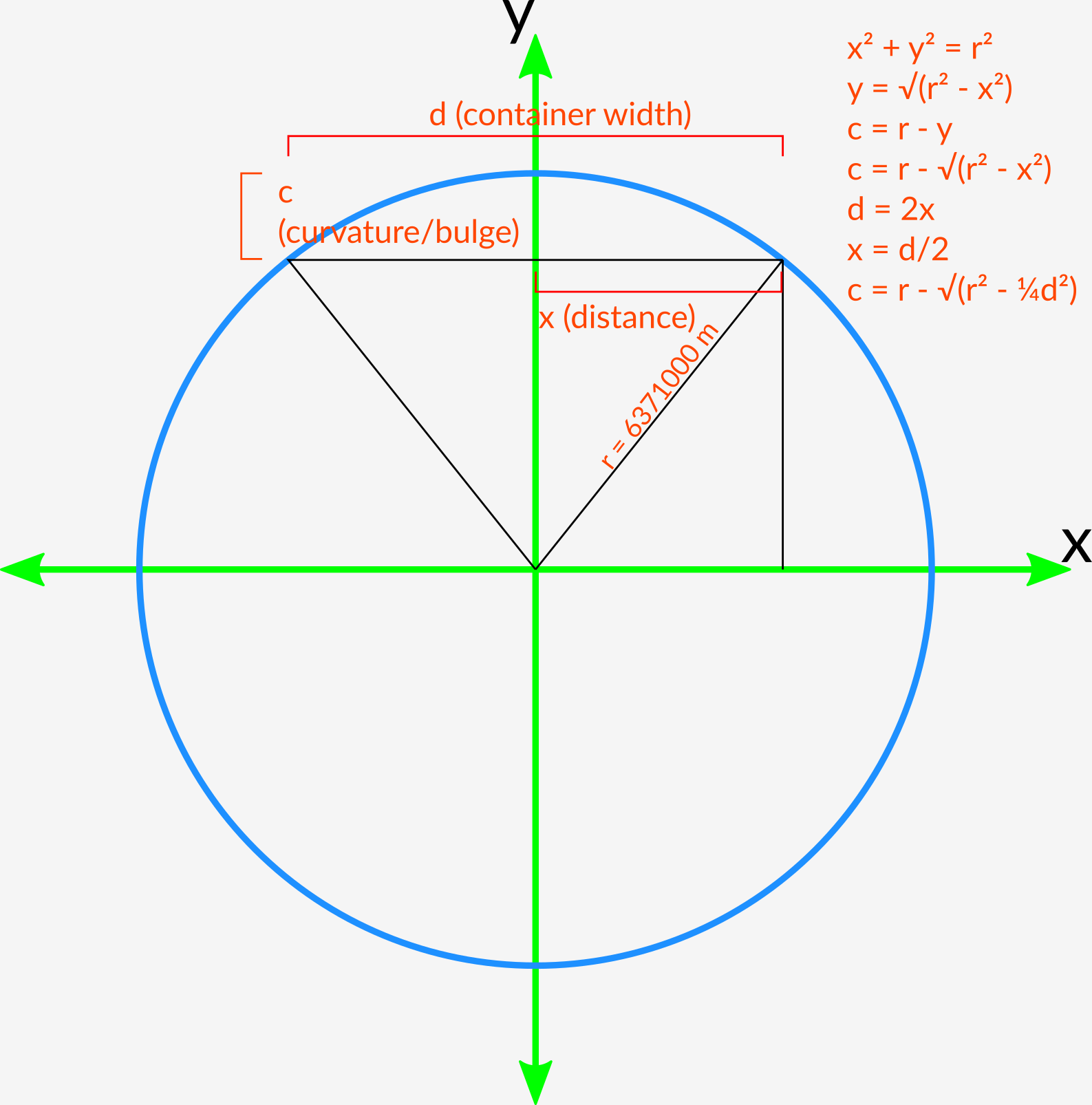
If the length of the horizon is 5048m, then the bulge in the middle is: 6371000 – sqrt(6371000^2 – 0.25 * 5425 ^ 2) = 0.577 m.

References